Solving the Pandigital Puzzle with AVX2 SIMD Acceleration.

Shai Asher

21 Jul 2025 • 3 min read

Using AVX2 SIMD instructions in C++ to accelerate the search for the largest 1-9 pandigital concatenated product.

If you've ever tackled Project Euler Problem 38, you're likely familiar with the hunt for the largest 1-to-9 pandigital number that can be formed by concatenating the product of an integer with (1, 2, ..., n).

But what happens when we bring SIMD acceleration into the equation?

In this blog post, we'll explore how AVX2 instructions can be harnessed using C++ to greatly optimize the search process. Let’s break down the solution, understand its components, and explore how it improves on scalar counterparts.

What is AVX2 and SIMD?

AVX2 (Advanced Vector Extensions 2) is a set of CPU instructions that allow for SIMD (Single Instruction, Multiple Data) parallelism. This means that a single operation can be applied to multiple data points simultaneously.

With AVX2, we get:

256-bit registers
Integer and floating-point arithmetic
Efficient data packing/unpacking

Diagram: SIMD vs Scalar Execution

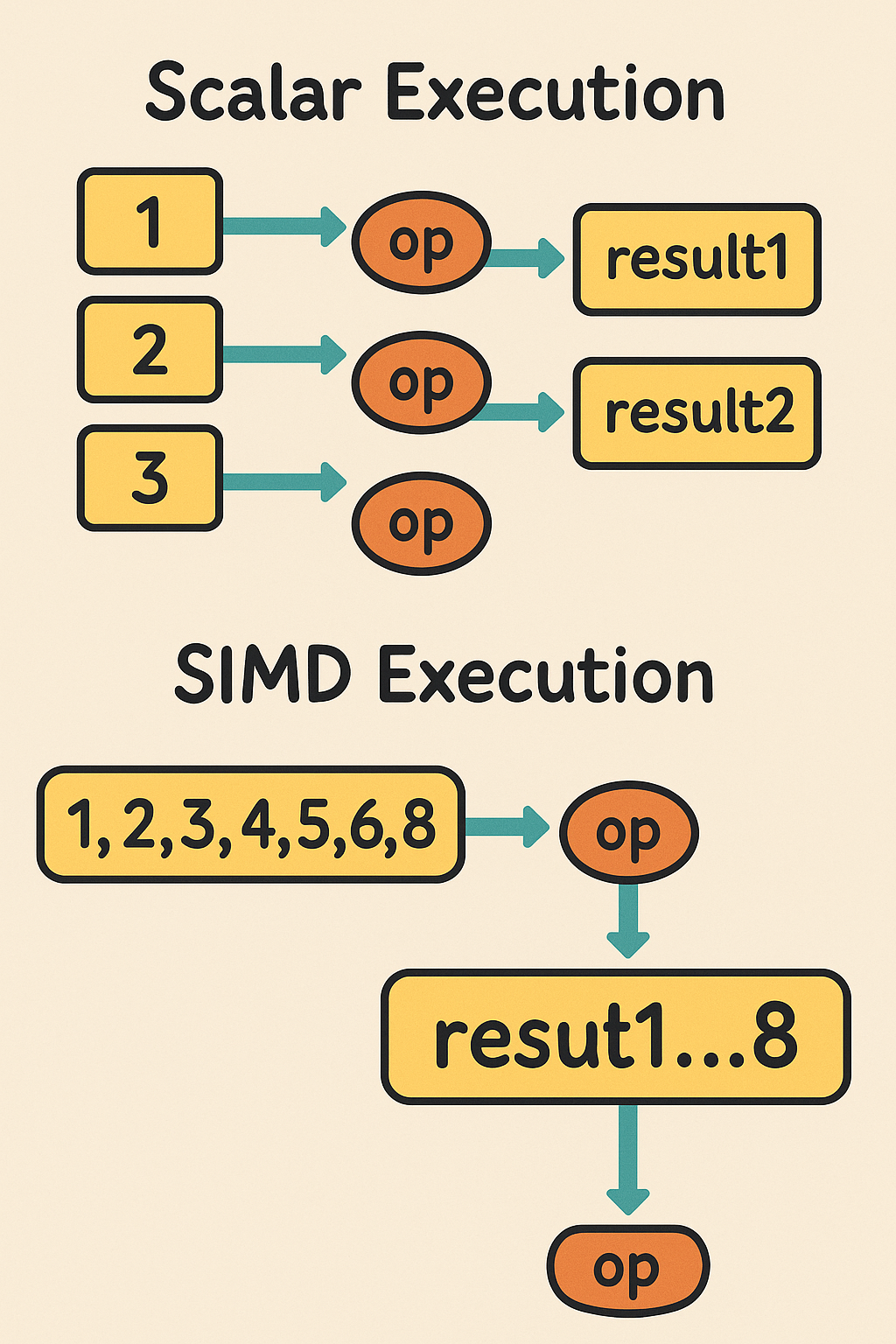
Diagram: AVX2 Register Visualization

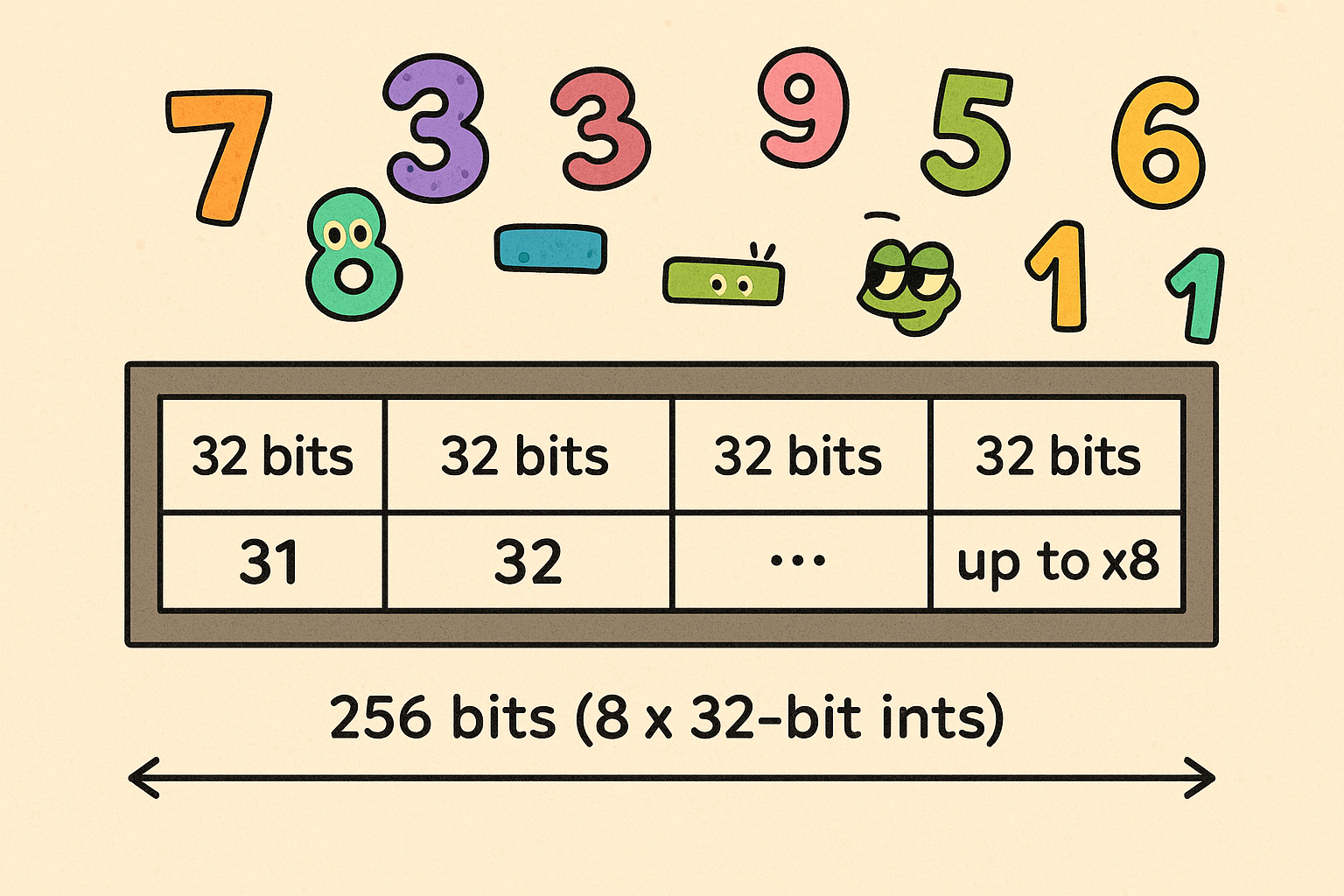
SIMD is particularly beneficial for workloads that involve repeating the same operation across a dataset, exactly the case when we're checking thousands of k values.

Problem Recap: What is a Pandigital Concatenated Product?

We're looking for the largest number that:

Uses each digit from 1 to 9 exactly once (no 0s, no duplicates)
It is formed by concatenating k * 1, k * 2, ..., k * n for some integer k
Commonly, the maximum n That makes sense, it's 2 for 4-digit k

Example:

k = 9327:
k * 1 = 9327
k * 2 = 18654
=> Concatenation = 932718654 (which is 1-9 pandigital)

Overview of the SIMD Approach

Features

AVX2 vectorization: Processes 8 values in parallel
32-byte aligned memory: Ensures optimal use of AVX registers
Hybrid architecture: SIMD for computation, scalar code for validation

Code Summary

constexpr int MAX_K = 9999;
CalcResult result = {0, 0, 2}; // maxVal, bestK, bestN

alignas(32) int kArr[8];
__m256i two = _mm256_set1_epi32(2);

for (int k = 1; k <= MAX_K; k += 8) {
    // Fill array with values k..k+7
    // SIMD compute: k*1 and k*2 using AVX2
    // Store results into prod1 and prod2
    // Scalar: Concatenate results, check pandigital, update max
}

Key Optimizations

1. AVX2 Vector Multiplication

By loading 8 integers into a 256-bit AVX2 register, we compute 8 k*2 values in parallel using _mm256_mullo_epi32.

2. Efficient String Concatenation

Instead of using std::to_string or streams, we use snprintf:

char s[10];
snprintf(s, sizeof(s), "%d%d", p1, p2);

This avoids heap allocations and improves performance in hot loops.

3. Fast Pandigital Check

The isPandigital The function avoids dynamic memory and checks for digit uniqueness using a simple boolean array.

Performance Characteristics

Time Complexity: O((n/8) * log n)
Cache Usage: ~96 bytes per iteration (3 aligned arrays)
CPU Requirement: AVX2-capable processor

Final Thoughts

This approach is not just fast — it’s fun. Writing high-performance code that leverages your CPU's full capabilities is immensely satisfying, and using SIMD for a problem like this makes it feel like solving a puzzle with rocket fuel.

If you're eager to squeeze every cycle out of your code, consider using AVX2 SIMD. You'll never look at loops the same way again.

Source Code

You can find the code on GitHub. This file is part of the project to compare different implementations solving this problem in C++.